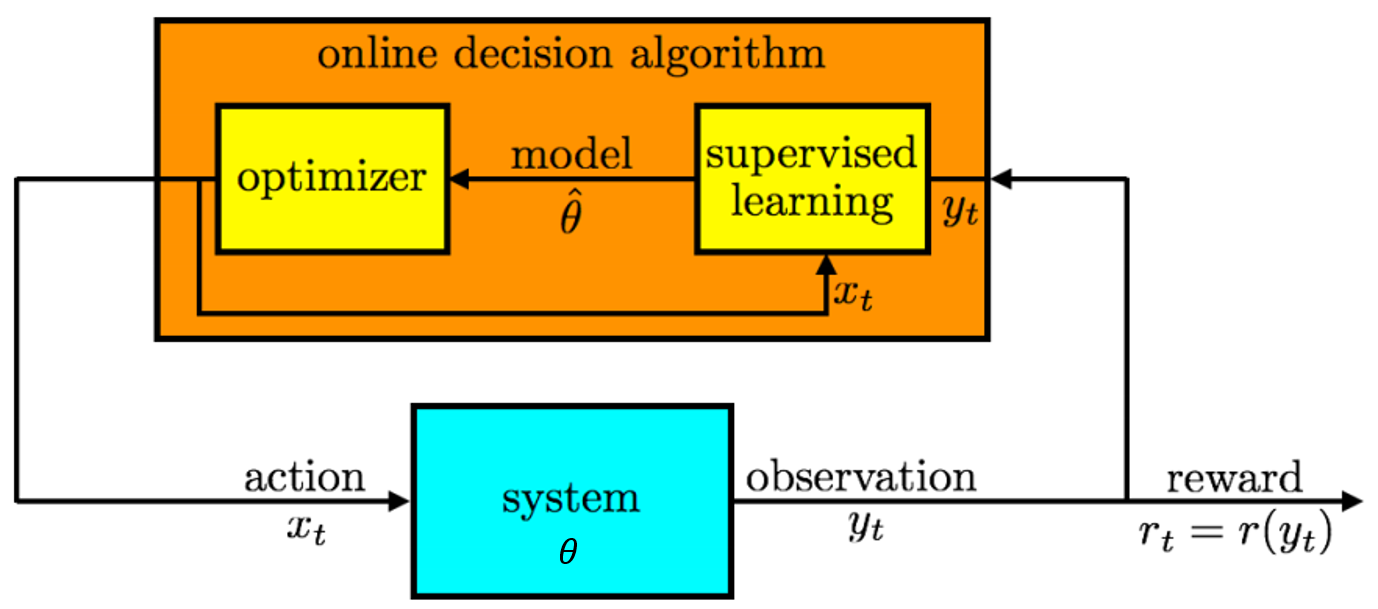
Introduction to Thompson Sampling¶
Bernoulli Bandit Problem¶
- K Bandits
- T periods
- For No.i bandit, reward 1 with probability $\theta_i, 0$ with $1-\theta_i$

- Prior: $$ p_{\theta_k}(x)=\frac{\Gamma(\alpha_k+\beta_k)}{\Gamma(\alpha_k)\Gamma(\beta_k)} x^{\alpha_k-1}(1-x)^{\beta_k-1} $$
- Likelihood: $$ p(y_t|\theta_k)=\theta^{y_t}_k(1-\theta_{k})^{1-y_t} $$
- Bayesian Update for Beta-Bernoulli: $$ (\alpha_k,\beta_k)\leftarrow \left \{ \begin{aligned} (\alpha_k,\beta_k),& & if\ x_t\neq k \\ (\alpha_k,\beta_k)+(r_t,1-r_t),& & if \ x_t=k \end{aligned} \right. $$
- Greedy Algorithm/ $\epsilon$-Greedy Algorithm: $\hat{\theta}=\mathbb{E}(\theta_k)$
- Thompson Sampling Algorithm: $\hat{\theta}$ sample from $p_{\theta_k}$

In [ ]:
"""
Environment
"""
class FiniteArmedBernoulliBandit(Environment):
"""Simple N-armed bandit."""
def __init__(self, probs):
self.probs = np.array(probs)
assert np.all(self.probs >= 0)
assert np.all(self.probs <= 1)
self.optimal_reward = np.max(self.probs)
self.n_arm = len(self.probs)
def get_observation(self):
return self.n_arm
def get_optimal_reward(self):
return self.optimal_reward
def get_expected_reward(self, action):
return self.probs[action]
def get_stochastic_reward(self, action):
return np.random.binomial(1, self.probs[action])
In [ ]:
"""
Agent 1: Greedy
"""
class FiniteBernoulliBanditEpsilonGreedy(Agent):
"""Simple agent made for finite armed bandit problems."""
def get_posterior_mean(self):
return self.prior_success / (self.prior_success + self.prior_failure)
def get_posterior_sample(self):
return np.random.beta(self.prior_success, self.prior_failure)
def update_observation(self, observation, action, reward):
# Naive error checking for compatibility with environment
assert observation == self.n_arm
if np.isclose(reward, 1):
self.prior_success[action] += 1
elif np.isclose(reward, 0):
self.prior_failure[action] += 1
else:
raise ValueError('Rewards should be 0 or 1 in Bernoulli Bandit')
def pick_action(self, observation):
"""Take random action prob epsilon, else be greedy."""
if np.random.rand() < self.epsilon:
action = np.random.randint(self.n_arm)
else:
posterior_means = self.get_posterior_mean()
action = random_argmax(posterior_means)
return action
In [ ]:
"""
Agent 2: TS
"""
class FiniteBernoulliBanditTS(FiniteBernoulliBanditEpsilonGreedy):
"""Thompson sampling on finite armed bandit."""
def pick_action(self, observation):
"""Thompson sampling with Beta posterior for action selection."""
sampled_means = self.get_posterior_sample()
action = random_argmax(sampled_means)
return action
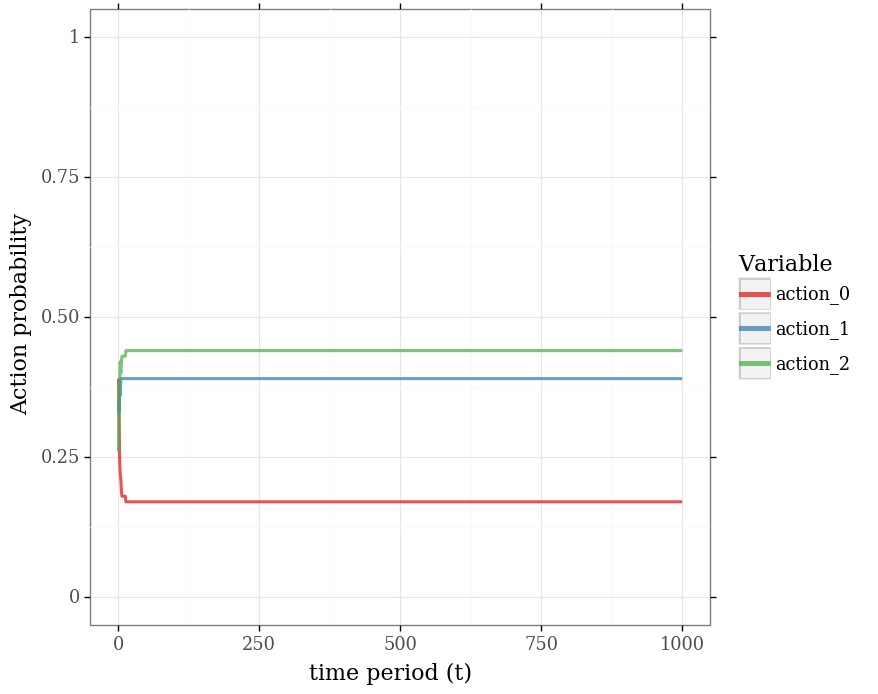
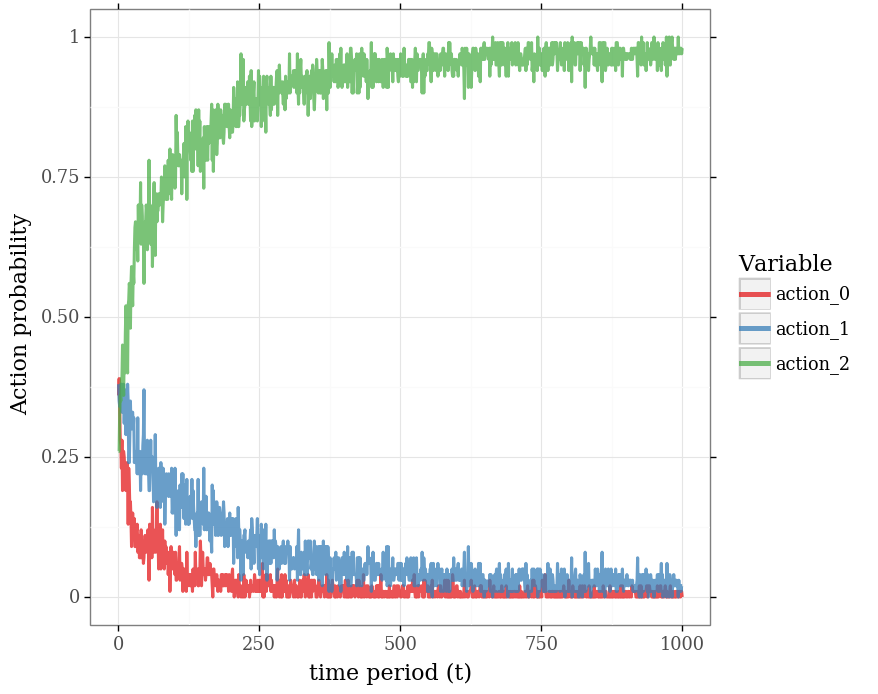
Approximations¶
1. Laplace Approximation¶
$$ ln(g(\phi))\approx ln(g(\overline{\phi}))-\frac{1}{2}(\phi-\overline{\phi})^T C (\phi-\overline{\phi}) $$where $\overline{\phi}$ is its mode and $C=-\nabla^2 ln(g(\overline{\phi}))$
$$g(\phi) \propto e^{-\frac{1}{2}(\phi-\overline{\phi})^T C (\phi-\overline{\phi})}$$
$$g(\phi) =\sqrt{\frac{C}{2\pi}}e^{-\frac{1}{2}(\phi-\overline{\phi})^T C (\phi-\overline{\phi})}$$
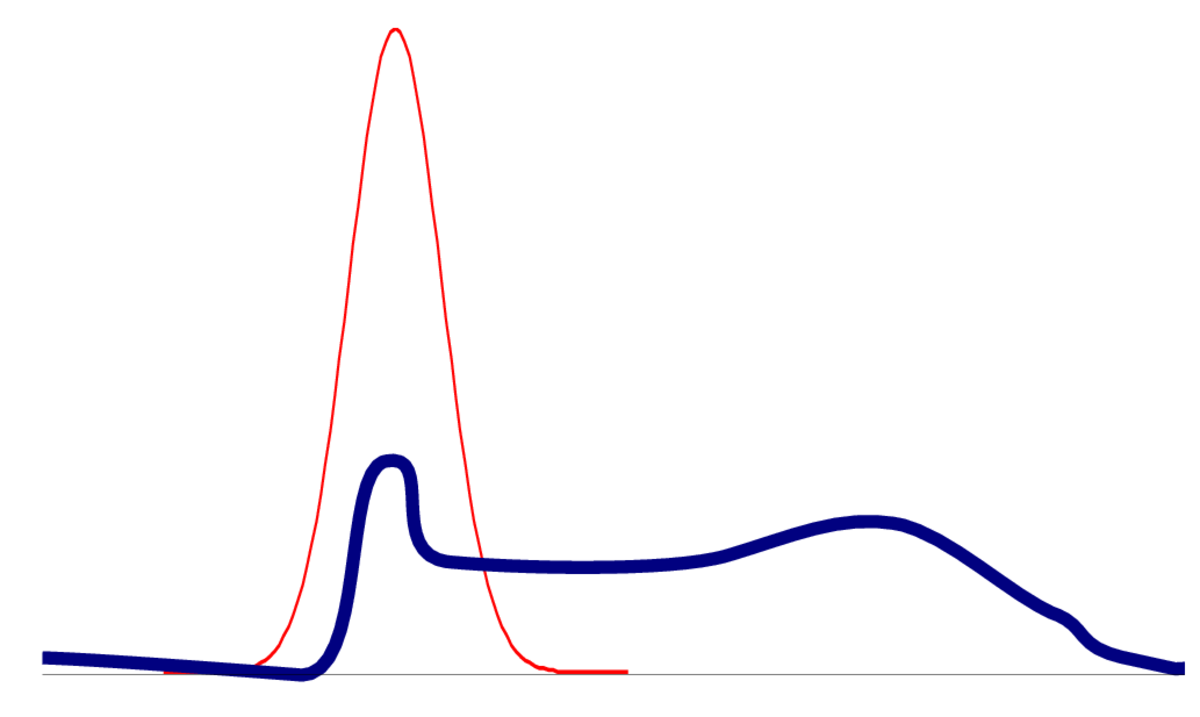
Bernoulli:
$$ \begin{aligned} f(\theta)&\propto \theta^s(1-\theta)^{n-s}\\ ln f(\theta)&=const+sln(\theta)+(n-s)ln(1-\theta)\\ \frac{dL(\theta)}{d\theta}&=\frac{s}{\theta}-\frac{n-s}{1-\theta}=0\rightarrow \theta_0=\frac{s}{n}=\overline{\phi}\\ \frac{d^2L(\theta)}{d\theta^2}&=-\frac{s}{\theta^2}-\frac{n-s}{(1-\theta)^2}=-\frac{n}{\theta(1-\theta)}=C\\ \end{aligned} $$In [ ]:
class FiniteBernoulliBanditLaplace(FiniteBernoulliBanditTS):
"""Laplace Thompson sampling on finite armed bandit."""
def get_posterior_sample(self):
"""Gaussian approximation to posterior density (match moments)."""
(a, b) = (self.prior_success + 1e-6 - 1, self.prior_failure + 1e-6 - 1)
# The modes are not well defined unless alpha, beta > 1
assert np.all(a > 0)
assert np.all(b > 0)
mode = a / (a + b)
#hessian = a / mode + b / (1 - mode)
hessian = (a+b)/(mode*(1-mode))
laplace_sample = mode + np.sqrt(1 / hessian) * np.random.randn(self.n_arm)
return laplace_sample
2. Langevin Monte Carlo¶
$$
d\phi_t=\nabla ln(g(\phi_t))dt+\sqrt{2}dB_t
$$
Euler discretization¶
$$ \phi_{n+1}=\phi_n+\epsilon\nabla ln(g(\phi_n))+\sqrt{2\epsilon}W_n $$Modification 1: Stochastic gradient Langevin Monte Carlo¶
Modification 2: Preconditioning matrix¶
$$
\phi_{n+1}=\phi_n+\epsilon A \nabla ln(g(\phi_n))+\sqrt{2\epsilon}AW_n
$$
where $A=-(\nabla^2 ln(g(\phi))|_{\phi=\phi_0})^{-1}$ and $W_n\sim N(0,1)$
How to understand
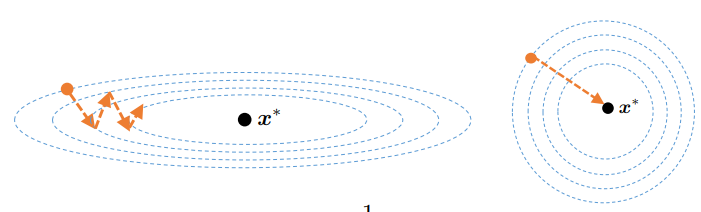
In [21]:
class FiniteBernoulliBanditLangevin(FiniteBernoulliBanditTS):
'''Langevin method for approximate posterior sampling.'''
def __init__(self,n_arm, step_count=1000,step_size=0.01,a0=1, b0=1, epsilon=0.0):
FiniteBernoulliBanditTS.__init__(self,n_arm, a0, b0, epsilon)
self.step_count = step_count
self.step_size = step_size
def project(self,x):
'''projects the vector x onto [_SMALL_NUMBER,1-_SMALL_NUMBER] to prevent
numerical overflow.'''
return np.minimum(1-_SMALL_NUMBER,np.maximum(x,_SMALL_NUMBER))
def compute_gradient(self,x):
grad = (self.prior_success-1)/x - (self.prior_failure-1)/(1-x)
return grad
def compute_preconditioners(self,x):
second_derivatives = (self.prior_success-1)/(x**2) + (self.prior_failure-1)/((1-x)**2)
second_derivatives = np.maximum(second_derivatives,_SMALL_NUMBER)
preconditioner = np.diag(1/second_derivatives)
preconditioner_sqrt = np.diag(1/np.sqrt(second_derivatives))
return preconditioner,preconditioner_sqrt
In [22]:
def get_posterior_sample(self):
(a, b) = (self.prior_success + 1e-6 - 1, self.prior_failure + 1e-6 - 1)
# The modes are not well defined unless alpha, beta > 1
assert np.all(a > 0)
assert np.all(b > 0)
x_map = a / (a + b)
x_map = self.project(x_map)
preconditioner, preconditioner_sqrt=self.compute_preconditioners(x_map)
x = x_map
for i in range(self.step_count):
g = self.compute_gradient(x)
scaled_grad = preconditioner.dot(g)
scaled_noise= preconditioner_sqrt.dot(np.random.randn(self.n_arm))
x = x + self.step_size*scaled_grad + np.sqrt(2*self.step_size)*scaled_noise
x = self.project(x)
return x
3. Bootstrapping¶
- Generate a hypothetical history $\mathbb{\hat{H}}_{t-1}=((\hat{x}_1,\hat{y}_1),\dots,(\hat{x}_{t-1},\hat{y}_{t-1}))$
- $Max_{\theta} \ \ \ Likehood(\theta)$
In [ ]:
class FiniteBernoulliBanditBootstrap(FiniteBernoulliBanditTS):
"""Bootstrapped Thompson sampling on finite armed bandit."""
def get_posterior_sample(self):
"""Use bootstrap resampling instead of posterior sample."""
total_tries = self.prior_success + self.prior_failure
prob_success = self.prior_success / total_tries
boot_sample = np.random.binomial(total_tries, prob_success) / total_tries
return boot_sample
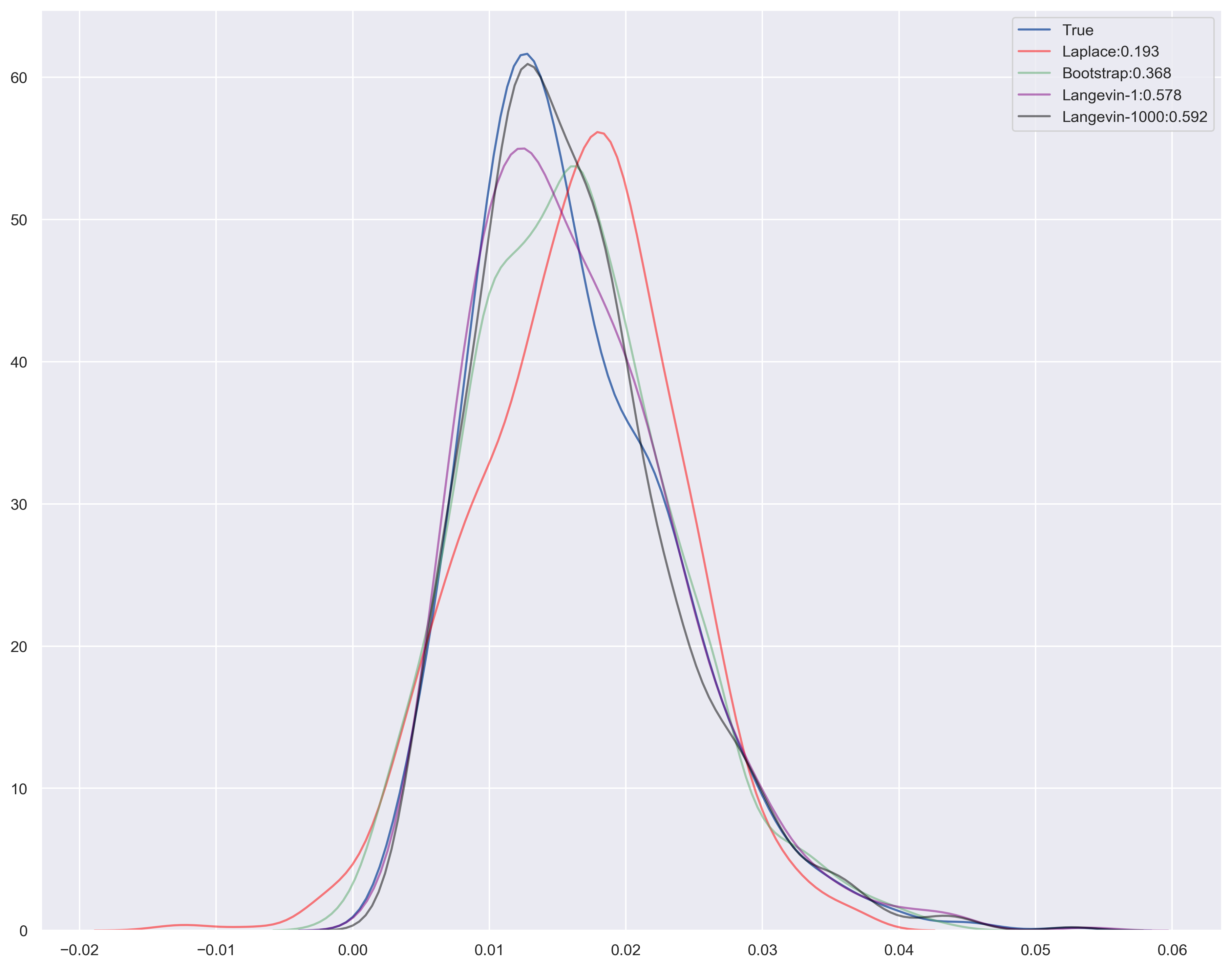
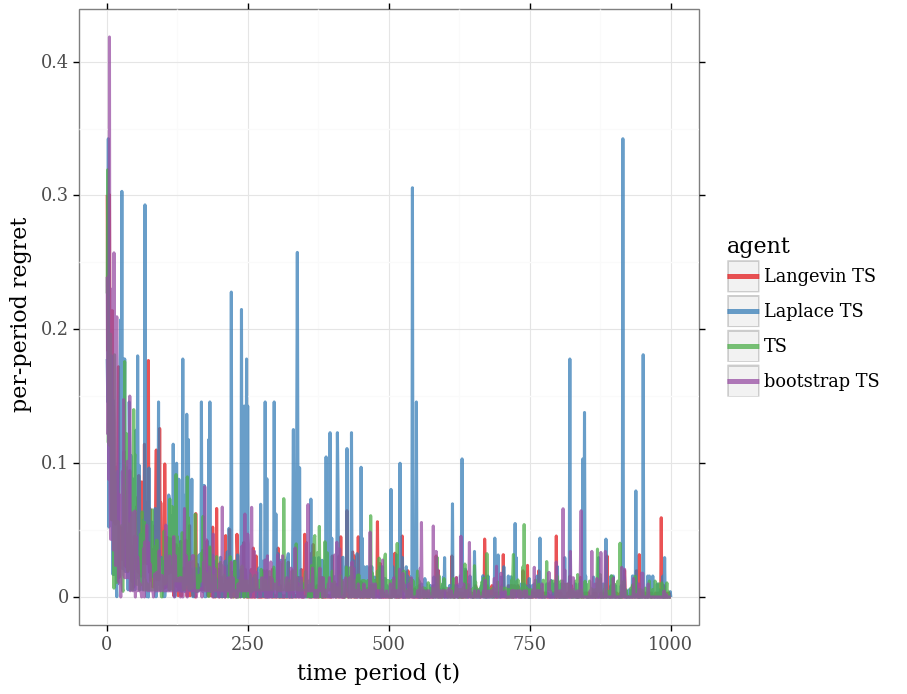
Incremental Implementation¶
Incremental version of the Laplace approximation $$ \begin{aligned} H_t=H_{t-1}+\nabla^2 g_t(\overline{\theta}_{t-1})\\ \overline{\theta}_t=\overline{\theta}_{t-1}-H_t^{-1}\nabla g_t(\overline{\theta}_{t-1}) \end{aligned} $$
where $g_t(\theta)=ln(l_t(\theta))$ and $\overline{\theta}_k=argmax_{\theta}g_k(\theta)$